Deep Learning Foundation
AI Okinawa
Jakub “Kuba” Kolodziejczyk
Profile
名前: Kuba Kolodziejczyk
出身: ポーランド
大学: ロンドン大学, 大阪大学
過去
Nanyang Technological University
OIST
レキサス
現在
AI Okinawa - 代表
LiLz株式会社 - CTO
琉球大学 - 非常勤講師
出身: ポーランド
大学: ロンドン大学, 大阪大学
過去
Nanyang Technological University
OIST
レキサス
現在
AI Okinawa - 代表
LiLz株式会社 - CTO
琉球大学 - 非常勤講師

What this course is about
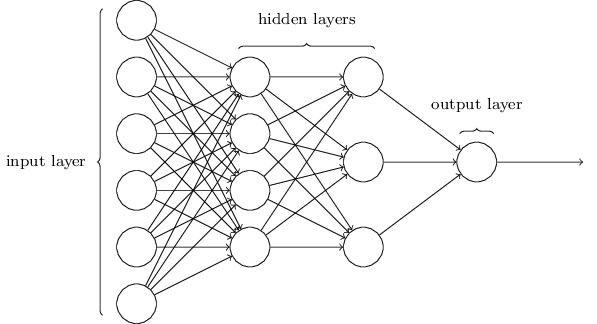
neuralnetworksanddeeplearning.com
Deep learning - short overview
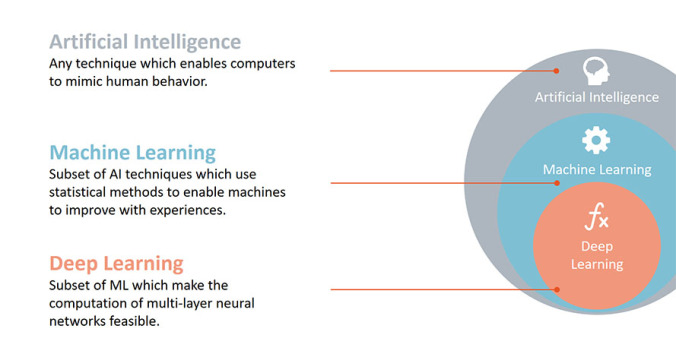
rapidminer.com
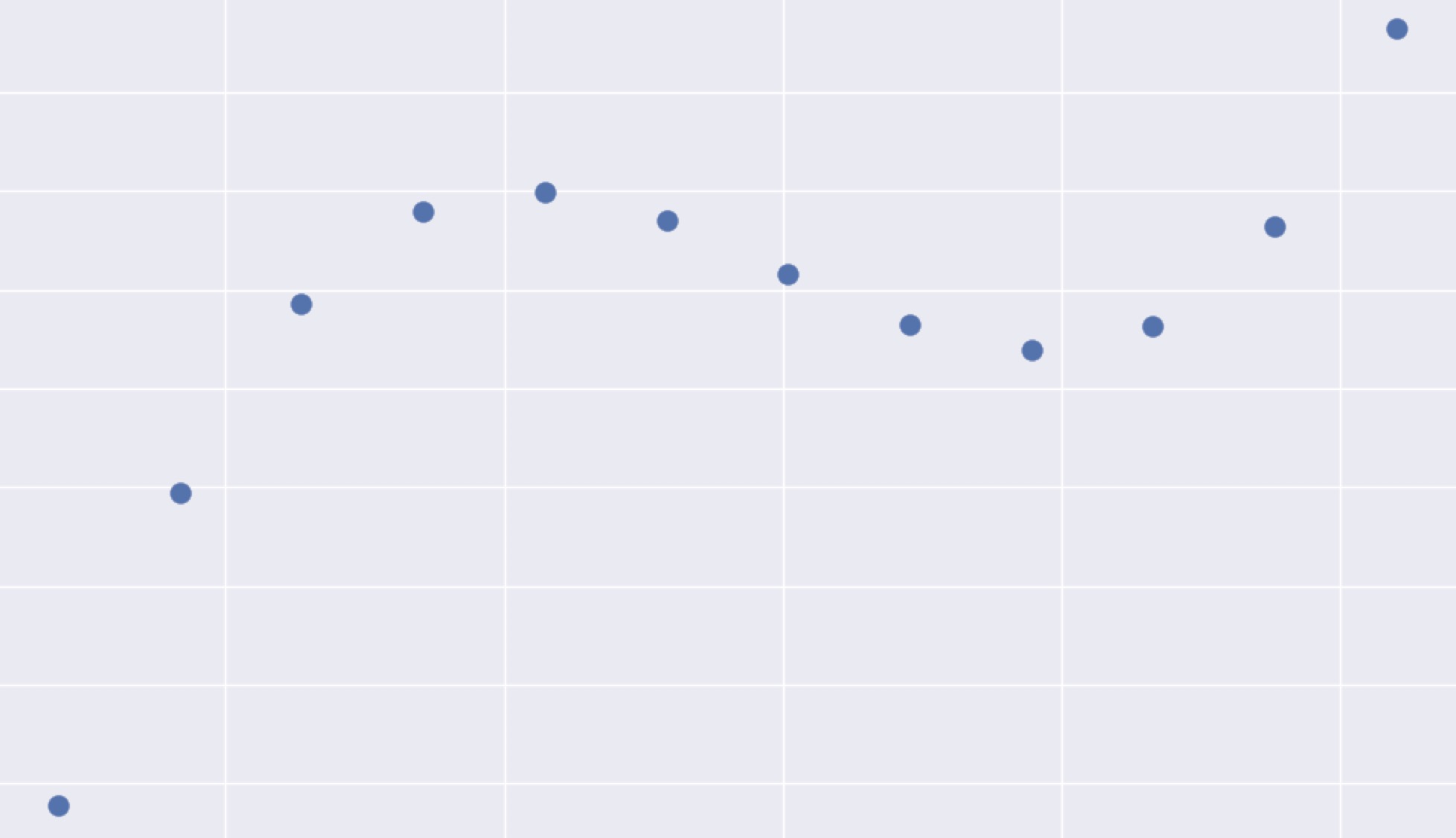
$$ y = ax^3 + bx^2 + cx + d$$

Ask questions
Take notes
Create a cheat-sheet
Derivatives review
- Derivatives notation
- Derivative definition
- What information derivatives give us?
- Differentiation of polynomials
- Derivative of \( y = e^x \)
- Derivative of a product of functions
- Derivative of a quotient of functions
- Derivative of a function of a function
- Derivative of \( y = ln(x) \)
- Derivative of \( y = ln(u) \)
Forward propagation

neuralnetworksanddeeplearning.com
- Simple neural network
- Inputs and outputs
- Weights and biases
- Preactivation
- Generic activation
- Sigmoid function
Sample forward propagation computations
| \( x_1 \) | \( 4 \) |
| \( x_2 \) | \( 0.5 \) |
| \( w_1 \) | \( 1 \) |
| \( w_2 \) | \( -1 \) |
| \( b \) | \( -2 \) |
Preactivation
$$ z = (w_1 * x_1) + (w_2 * x_2) + b $$
$$ z = (1 * 4) + (-1 * 0.5) - 2 $$
$$ z = 4 - 0.5 - 2 = 1.5 $$
Activation
$$ a = \sigma(z) = \frac{1}{1 + e^{-z}} $$
$$ a = \sigma(1.5) = \frac{1}{1 + e^{-1.5}} $$
$$ a = 0.82 $$
Cost function
- Why use cost function?
- Gradient descent
Cost derivative with respect to activation
$$ C = \frac{1}{2} (y - a)^2 $$
Call
$$ u = y - a $$
Then
$$ C = \frac{1}{2} u^2 $$
$$ \frac{ \partial{C} }{ \partial{a} } = \frac{ \partial{C} }{ \partial{u} } * \frac{ \partial{u} }{ \partial{a} } $$ $$ \frac{ \partial{C} }{ \partial{u} } = \frac{1}{2} * 2u = u $$ $$ \frac{ \partial{u} }{ \partial{a} } = -1 $$ $$ \frac{ \partial{C} }{ \partial{a} } = -u = -(y - a) = a - y $$
$$ \frac{ \partial{C} }{ \partial{a} } = a - y $$
Cost derivative with respect to preactivation
$$ \frac { \partial{C} }{ \partial{z} } = \frac { \partial{C} }{ \partial{a} } * \frac { \partial{a} }{ \partial{z} }$$
$$ a = \frac{1}{ 1 + e^{-z} } $$
Call
$$ f = 1 $$
$$ g = 1 + e^{-z} $$
$$ a = \frac{f}{g} $$Then
$$
\frac{ \partial{a} }{ \partial{z} } =
\frac{ \frac{\partial{f}}{\partial{z}} * g - f * \frac{\partial{g}}{\partial{z}}}{g^2}
$$
$$ \frac{ \partial{f} }{ \partial{z} } = 0 $$
Call
$$ u = -z $$
Then
$$ g = 1 + e^u $$
$$
\frac{ \partial{g} }{ \partial{z} } = \frac{ \partial{g} }{ \partial{u} } * \frac{ \partial{u} }{ \partial{z} }
$$
$$
\frac{ \partial{g} }{ \partial{u} } = e^u
$$
$$
\frac{ \partial{u} }{ \partial{z} } = -1
$$
$$
\frac{ \partial{g} }{ \partial{z} } = e^u * (-1)
$$
$$
\frac{ \partial{g} }{ \partial{z} } = -e^{-z}
$$
$$ \frac{ \partial{a} }{ \partial{z} } = \frac{ \frac{ \partial{f} }{ \partial{z} } * g - f * \frac{ \partial{g} }{ \partial{z} } } {g^2} $$ $$ \frac{ \partial{a} }{ \partial{z} } = \frac { 0 - 1 * (-e^{-z})} { (1 + e^{-z})^2 } $$ $$ \frac{ \partial{a} }{ \partial{z} } = \frac { e^{-z}} { (1 + e^{-z})^2 } $$
$$ a * (1 - a) = \frac{1}{ 1 + e^{-z} } * (1 - \frac{1}{ 1 + e^{-z} }) $$ $$ a * (1 - a) = \frac{1}{ 1 + e^{-z} } * (\frac {1 + e^{-z} }{ 1 + e^{-z} } - \frac{1}{ 1 + e^{-z} }) $$ $$ a * (1 - a) = \frac{1}{ 1 + e^{-z} } * \frac{ 1 + e^{-z} - 1 }{ 1 + e^{-z} } $$ $$ a * (1 - a) = \frac{1}{ 1 + e^{-z} } * \frac{ e^{-z} }{ 1 + e^{-z} } $$ $$ a * (1 - a) = \frac{ e^{-z} }{ (1 + e^{-z})^2 } $$
Therefore
$$
\frac{ \partial{a} }{ \partial{z} } = a * (1 - a)
$$
$$ \frac { \partial{C} }{ \partial{z} } = \frac { \partial{C} }{ \partial{a} } * a * (1 - a) $$
Cost derivative with respect to parameters
- Cost derivative with respect to weights
- Cost derivative with respect to bias
Parameters update
- Learning rate
- Weights update
- Bias update
One step of training algorithm
| \( x_1 \) | \( 4 \) |
| \( x_2 \) | \( 0.5 \) |
| \( w_1 \) | \( 1 \) |
| \( w_2 \) | \( -1 \) |
| \( b \) | \( -2 \) |
Preactivation
$$ z = (w_1 * x_1) + (w_2 * x_2) + b $$
$$ z = (1 * 4) + (-1 * 0.5) - 2 $$
$$ z = 4 - 0.5 - 2 = 1.5 $$
Activation
$$ a = \sigma(z) = \frac{1}{1 + e^{-z}} $$
$$ a = \sigma(1.5) = \frac{1}{1 + e^{-1.5}} $$
$$ a = 0.82 $$
Ground truth
$$ y = 1 $$
Cost
$$ C = \frac {1}{2} (y - a)^2 $$
$$ C = \frac {1}{2} (1 - 0.82)^2 = \frac {1}{2} (0.18)^2 = \frac {1}{2} * 0.0324 $$
$$ C = 0.0162 $$
Cost derivative with respect to activation
$$ \frac { \partial{C} }{ \partial{a} } = a - y $$
$$ \frac { \partial{C} }{ \partial{a} } = 0.82 - 1 $$
$$ \frac { \partial{C} }{ \partial{a} } = -0.18 $$
Cost derivative with respect to preactivation
$$ \frac { \partial{C} }{ \partial{z} } = \frac { \partial{C} }{ \partial{a} } * \frac { \partial{a} }{ \partial{z} } $$
$$ \frac { \partial{C} }{ \partial{a} } = -0.18 $$
$$ \frac { \partial{a} }{ \partial{z} } = a * (1 - a) $$ $$ \frac { \partial{a} }{ \partial{z} } = 0.82 * (1 - 0.82) = 0.82 * 0.18 $$ $$ \frac { \partial{a} }{ \partial{z} } \approx 0.15 $$
$$ \frac { \partial{C} }{ \partial{z} } = \frac { \partial{C} }{ \partial{a} } * \frac { \partial{a} }{ \partial{z} } $$ $$ \frac { \partial{C} }{ \partial{z} } = -0.18 * 0.15 $$ $$ \frac { \partial{C} }{ \partial{z} } = -0.027 $$
Cost derivative with respect to weight \( w_1 \)
$$ \frac { \partial{C} }{ \partial{w_1} } = \frac { \partial{C} }{ \partial{z} } * \frac { \partial{z} }{ \partial{w_1} } $$
$$ \frac { \partial{C} }{ \partial{z} } = -0.027 $$ $$ \frac { \partial{z} }{ \partial{w_1} } = x_1 = 4$$ $$ \frac { \partial{C} }{ \partial{w_1} } = -0.027 * 4 = -0.108 $$
Cost derivative with respect to weight \( w_2 \)
$$ \frac { \partial{C} }{ \partial{w_2} } = \frac { \partial{C} }{ \partial{z} } * \frac { \partial{z} }{ \partial{w_2} } $$
$$ \frac { \partial{C} }{ \partial{z} } = -0.027 $$ $$ \frac { \partial{z} }{ \partial{w_2} } = x_2 = 0.5 $$ $$ \frac { \partial{C} }{ \partial{w_2} } = -0.027 * 0.5 = -0.0135 $$
Cost derivative with respect to bias
$$ \frac { \partial{C} }{ \partial{b} } = \frac { \partial{C} }{ \partial{z} } * \frac { \partial{z} }{ \partial{b} } $$
$$ \frac { \partial{C} }{ \partial{z} } = -0.027 $$
$$ \frac { \partial{z} }{ \partial{b} } = 1 $$
$$ \frac { \partial{C} }{ \partial{b} } = -0.027 * 1 = -0.027 $$
Parameters updates
$$ \alpha = 1 $$
$$ w_1' = w_1 - \alpha * \frac { \partial{C} }{ \partial{w_1} } $$ $$ w_1' = 1 - 1 * (-0.108) = 1.108 $$
$$ w_2' = w_2 - \alpha * \frac { \partial{C} }{ \partial{w_2} } $$ $$ w_2' = -1 - 1 * (-0.0135) = -0.9865 $$
$$ b' = b - \alpha * \frac { \partial{C} }{ \partial{b} } $$ $$ b' = -2 - 1 * (-0.027) = -1.973 $$
After one step of training
| \( x_1 \) | \( 4 \) |
| \( x_2 \) | \( 0.5 \) |
| \( w_1 \) | \( 1.108 \) |
| \( w_2 \) | \( -0.9865 \) |
| \( b \) | \( -1.973 \) |
Preactivation
$$ z = (w_1 * x_1) + (w_2 * x_2) + b $$
$$ z = (1.108 * 4) + (-0.9865 * 0.5) - 1.973 $$
$$ z = 4.432 - 0.49325 - 1.973 = 1.96575 $$
Activation
$$ a = \sigma(z) = \frac{1}{1 + e^{-z}} $$
$$ a = \sigma(1.96575) = \frac{1}{1 + e^{-1.96575}} $$
$$ a = 0.88 $$
Networks with multiple outputs
- Parameters notation in complex networks
- One-hot encoding
- Computing cost over multiple outputs
Backpropagation - complex networks
- Cost derivative w.r.t. hidden node activation
- Compute layer error on node with multiple children
Matrix review
Matrix multiplication
$$
A\mathbf{x} =
\begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{bmatrix}
\begin{bmatrix}
x_{1} \\
x_{2} \\
x_{3} \\
\end{bmatrix} =
\begin{bmatrix}
(a_{11} * x_{1}) + (a_{12} * x_{2}) + (a_{13} x_{3}) \\
(a_{21} * x_{1}) + (a_{22} * x_{2}) + (a_{23} x_{3}) \\
(a_{31} * x_{1}) + (a_{32} * x_{2}) + (a_{33} x_{3}) \\
\end{bmatrix}
$$
$$
A\mathbf{x} =
\begin{bmatrix}
y_{1} \\
y_{2} \\
y_{3} \\
\end{bmatrix} = \mathbf{y}
$$
Derivative of a vector with respect to a scalar
$$
\mathbf{f} =
\begin{bmatrix}
f_{1} \\
f_{2} \\
f_{3} \\
\end{bmatrix} =
\begin{bmatrix}
2x - 3 \\
x^2 + 4 \\
8 \\
\end{bmatrix}
$$
$$
\frac{ \partial{\mathbf{f}} }{ \partial{x} } =
\begin{bmatrix}
\frac{ \partial{f_{1}} }{ \partial{x} } \\
\frac{ \partial{f_{2}} }{ \partial{x} } \\
\frac{ \partial{f_{3}} }{ \partial{x} } \\
\end{bmatrix} =
\begin{bmatrix}
2 \\
2x \\
0 \\
\end{bmatrix}
$$
Derivative of a scalar with respect to a vector
$$ f = 3x_{1} - x_{2}^2 + 4 $$
$$
\nabla{_\mathbf{x} f} =
\begin{bmatrix}
\frac{ \partial{f} }{ \partial{x_{1}} } \\
\frac{ \partial{f} }{ \partial{x_{2}} } \\
\frac{ \partial{f} }{ \partial{x_{3}} } \\
\end{bmatrix} =
\begin{bmatrix}
3 \\
-2x_{2} \\
0 \\
\end{bmatrix}
$$
Matrix notation - forward pass
Preactivation
$$
\mathbf{z^1} =
\begin{bmatrix}
z_{1}^1 \\
z_{2}^1 \\
z_{3}^1 \\
\end{bmatrix} =
\begin{bmatrix}
(w_{1,1}^1 a_{1}^0) + (w_{1,2}^1 a_{2}^0) + b_{1}^1 \\
(w_{2,1}^1 a_{1}^0) + (w_{2,2}^1 a_{2}^0) + b_{2}^1 \\
(w_{3,1}^1 a_{1}^0) + (w_{3,2}^1 a_{2}^0) + b_{3}^1 \\
\end{bmatrix}
$$
$$ \mathbf{z^1} = \begin{bmatrix} w_{1,1}^1 & w_{1,2}^1 \\ w_{2,1}^1 & w_{2,2}^1 \\ w_{3,1}^1 & w_{3,2}^1 \\ \end{bmatrix} \begin{bmatrix} a_{1}^0 \\ a_{2}^0 \\ \end{bmatrix} + \begin{bmatrix} b_{1}^1 \\ b_{2}^1 \\ b_{3}^1 \\ \end{bmatrix} $$
$$ \mathbf{z^1} = W^1 \mathbf{a^0} + \mathbf{b^1} $$
Generic form
$$ \mathbf{z^k} = W^k \mathbf{a^{k-1}} + \mathbf{b^k} $$
Activation
$$
\mathbf{a^k} =
\begin{bmatrix}
a_{1}^k \\
a_{2}^k \\
a_{3}^k \\
\end{bmatrix} =
\begin{bmatrix}
a(z_{1}^k) \\
a(z_{2}^k) \\
a(z_{3}^k) \\
\end{bmatrix}
$$
$$ \mathbf{a^k} = a( \mathbf{z^k} ) $$
Matrix notation backpropagation
Derivative of cost w.r.t. last activation vector
Derivative of cost w.r.t. last activation vector
$$ \nabla{_\mathbf{a^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{a_{1}^2} } \\ \frac{ \partial{C} }{ \partial{a_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{C_{1}} } * \frac{ \partial{C_{1}} }{ \partial{a_{1}^2} } \\ \frac{ \partial{C} }{ \partial{C_{2}} } * \frac{ \partial{C_{2}} }{ \partial{a_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^2} C} = \begin{bmatrix} \frac{1}{2} * (a_{1}^2 - y_{1}) \\ \frac{1}{2} * (a_{2}^2 - y_{2}) \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^2} C} = \frac{1}{2} * \begin{bmatrix} a_{1}^2 - y_{1} \\ a_{2}^2 - y_{2} \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^2} C} = \frac{1}{2} * (\mathbf{a^2} - \mathbf{y}) $$
Generic form
$$ \nabla{_\mathbf{a^K} C} = \frac{1}{m} * (\mathbf{a^K} - \mathbf{y}) $$
Matrix notation backpropagation
Derivative of cost w.r.t. preactivation vector
Derivative of cost w.r.t. preactivation vector
$$ \nabla{_\mathbf{z^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{z^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{a_{1}^2} } * \frac{ \partial{a_{1}^2} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{a_{2}^2} } * \frac{ \partial{a_{2}^2} }{ \partial{z_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{z^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{a_{1}^2} } * a_{1}^2 * (1 - a_{1}^2) \\ \frac{ \partial{C} }{ \partial{a_{2}^2} } * a_{2}^2 * (1 - a_{2}^2) \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{z^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{a_{1}^2} } \\ \frac{ \partial{C} }{ \partial{a_{2}^2} } \\ \end{bmatrix} \odot \begin{bmatrix} a_{1}^2 \\ a_{2}^2 \\ \end{bmatrix} \odot \begin{bmatrix} 1 - a_{1}^2 \\ 1 - a_{2}^2 \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{z^2} C} = \nabla{_\mathbf{a^2} C} \odot \mathbf{a^2} \odot (\mathbf{1} - \mathbf{a^2}) $$
Generic form
$$ \nabla{_\mathbf{z^k} C} = \nabla{_\mathbf{a^k} C} \odot \mathbf{a^k} \odot (\mathbf{1} - \mathbf{a^k}) $$
Matrix notation backpropagation
Derivative of cost w.r.t. hidden layer's activation vector
Derivative of cost w.r.t. hidden layer's activation vector
$$ \nabla{_\mathbf{a^1} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{a_{1}^1} } \\ \frac{ \partial{C} }{ \partial{a_{2}^1} } \\ \frac{ \partial{C} }{ \partial{a_{3}^1} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^1} C} = \begin{bmatrix} (\frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{a_{1}^1} }) + (\frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{a_{1}^1} }) \\ (\frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{a_{2}^1} }) + (\frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{a_{2}^1} }) \\ (\frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{a_{3}^1} }) + (\frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{a_{3}^1} }) \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^1} C} = \begin{bmatrix} (\frac{ \partial{C} }{ \partial{z_{1}^2} } * w_{11}^2) + (\frac{ \partial{C} }{ \partial{z_{2}^2} } * w_{21}^2) \\ (\frac{ \partial{C} }{ \partial{z_{1}^2} } * w_{12}^2) + (\frac{ \partial{C} }{ \partial{z_{2}^2} } * w_{22}^2) \\ (\frac{ \partial{C} }{ \partial{z_{1}^2} } * w_{13}^2) + (\frac{ \partial{C} }{ \partial{z_{2}^2} } * w_{23}^2) \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{a^1} C} = \begin{bmatrix} w_{11}^2 & w_{21}^2 \\ w_{12}^2 & w_{22}^2 \\ w_{13}^2 & w_{23}^2 \\ \end{bmatrix} * \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } \end{bmatrix} $$
$$ \nabla{_\mathbf{a^1} C} = \begin{bmatrix} w_{11}^2 & w_{12}^2 & w_{13}^2 \\ w_{21}^2 & w_{22}^2 & w_{23}^2 \\ \end{bmatrix}^T * \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } \end{bmatrix} $$
$$ \nabla{_\mathbf{a^1} C} = {W^2}^T * \nabla{_\mathbf{z^2} C} $$
Generic form
$$ \nabla{_\mathbf{a^k} C} = {W^{k+1}}^T * \nabla{_\mathbf{z^{k+1}} C} $$
Matrix notation backpropagation
Derivative of cost w.r.t. weights matrix
Derivative of cost w.r.t. weights matrix
$$ \frac{ \partial{C} }{ \partial{W^2} } = \begin{bmatrix} \frac{ \partial{C} }{ \partial{W_{11}^2} } & \frac{ \partial{C} }{ \partial{W_{12}^2} } & \frac{ \partial{C} }{ \partial{W_{13}^2} } \\ \frac{ \partial{C} }{ \partial{W_{21}^2} } & \frac{ \partial{C} }{ \partial{W_{22}^2} } & \frac{ \partial{C} }{ \partial{W_{23}^2} } \\ \end{bmatrix} $$
$$ \frac{ \partial{C} }{ \partial{W^2} } = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{W_{11}^2} } & \frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{W_{12}^2} } & \frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{W_{13}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{W_{21}^2} } & \frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{W_{22}^2} } & \frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{W_{23}^2} } \\ \end{bmatrix} $$
$$ \frac{ \partial{C} }{ \partial{W^2} } = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } * a_{1}^1 & \frac{ \partial{C} }{ \partial{z_{1}^2} } * a_{2}^1 & \frac{ \partial{C} }{ \partial{z_{1}^2} } * a_{3}^1 \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } * a_{1}^1 & \frac{ \partial{C} }{ \partial{z_{2}^2} } * a_{2}^1 & \frac{ \partial{C} }{ \partial{z_{2}^2} } * a_{3}^1 \\ \end{bmatrix} $$
$$ \frac{ \partial{C} }{ \partial{W^2} } = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } \\ \end{bmatrix} * \begin{bmatrix} a_{1}^1 & a_{2}^1 & a_{3}^1 \\ \end{bmatrix} $$
$$ \frac{ \partial{C} }{ \partial{W^2} } = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } \\ \end{bmatrix} * \begin{bmatrix} a_{1}^1 \\ a_{2}^1 \\ a_{3}^1 \\ \end{bmatrix}^T $$
$$ \frac{ \partial{C} }{ \partial{W^2} } = \nabla{_\mathbf{z^2} C} * \mathbf{a^1}^T $$
Generic form
$$ \frac{ \partial{C} }{ \partial{W^k} } = \nabla{_\mathbf{z^k} C} * \mathbf{a^{k-1}}^T $$
Weights updates
$$ W^{k'} = W^k - \alpha * \frac{ \partial{C} }{ \partial{W^k} } $$
Matrix notation backpropagation
Derivative of cost w.r.t. biases vector
Derivative of cost w.r.t. biases vector
$$ \nabla{_\mathbf{b^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{b_{1}^2} } \\ \frac{ \partial{C} }{ \partial{b_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{b^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } * \frac{ \partial{z_{1}^2} }{ \partial{b_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } * \frac{ \partial{z_{2}^2} }{ \partial{b_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{b^2} C} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } * 1 \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } * 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{ \partial{C} }{ \partial{z_{1}^2} } \\ \frac{ \partial{C} }{ \partial{z_{2}^2} } \\ \end{bmatrix} $$
$$ \nabla{_\mathbf{b^2} C} = \nabla{_\mathbf{z^2} C} $$
Generic form
$$ \nabla{_\mathbf{b^k} C} = \nabla{_\mathbf{z^k} C} $$
Weights updates
$$ \mathbf{b}^{k'} = \mathbf{b}^k - \alpha * \nabla{_\mathbf{b^k} C} $$
A simple neural network implementation
- MNIST dataset
- Training data vs test data
- Shuffling
- Forward stage
- Backpropagation
- Three qualities of deep learning
Neural network as universal function approximator
Approximating a function with strips
$$ z = wx + b $$ $$ a = \sigma(z) $$
Influence of weight on activation
Weight \( w = 1 \)
| input | preactivation | activation |
|---|---|---|
| \( x = -10 \) | \( z = -10 \) | \( a = 0 \) |
| \( x = -5 \) | \( z = -5 \) | \( a = 0.01 \) |
| \( x = -1 \) | \( z = -1 \) | \( a = 0.27 \) |
| \( x = -0.1 \) | \( z = -0.1 \) | \( a = 0.48 \) |
| \( x = -0.01 \) | \( z = -0.01 \) | \( a = 0.498 \) |
| \( x = 0 \) | \( z = 0 \) | \( a = 0.5 \) |
| \( x = 0.01 \) | \( z = 0.01 \) | \( a = 0.502 \) |
| \( x = 0.1 \) | \( z = 0.1 \) | \( a = 0.52 \) |
| \( x = 1 \) | \( z = 1 \) | \( a = 0.73 \) |
| \( x = 5 \) | \( z = 5 \) | \( a = 0.99 \) |
| \( x = 10 \) | \( z = 10 \) | \( a = 1 \) |
Weight \( w = 10 \)
| input | preactivation | activation |
|---|---|---|
| \( x = -10 \) | \( z = -100 \) | \( a = 0 \) |
| \( x = -5 \) | \( z = -50 \) | \( a = 0 \) |
| \( x = -1 \) | \( z = -10 \) | \( a = 0 \) |
| \( x = -0.1 \) | \( z = -1 \) | \( a = 0.27 \) |
| \( x = -0.01 \) | \( z = -0.1 \) | \( a = 0.48 \) |
| \( x = 0 \) | \( z = 0 \) | \( a = 0.5 \) |
| \( x = 0.01 \) | \( z = 0.1 \) | \( a = 0.502 \) |
| \( x = 0.1 \) | \( z = 1 \) | \( a = 0.73 \) |
| \( x = 1 \) | \( z = 10 \) | \( a = 1 \) |
| \( x = 5 \) | \( z = 50 \) | \( a = 1 \) |
| \( x = 10 \) | \( z = 100 \) | \( a = 1 \) |
Weight \( w = 100 \)
| input | preactivation | activation |
|---|---|---|
| \( x = -10 \) | \( z = -1000 \) | \( a = 0 \) |
| \( x = -5 \) | \( z = -500 \) | \( a = 0 \) |
| \( x = -1 \) | \( z = -100 \) | \( a = 0 \) |
| \( x = -0.1 \) | \( z = -10 \) | \( a = 0 \) |
| \( x = -0.01 \) | \( z = -1 \) | \( a = 0.27 \) |
| \( x = 0 \) | \( z = 0 \) | \( a = 0.5 \) |
| \( x = 0.01 \) | \( z = 1 \) | \( a = 0.73 \) |
| \( x = 0.1 \) | \( z = 10 \) | \( a = 1 \) |
| \( x = 1 \) | \( z = 100 \) | \( a = 1 \) |
| \( x = 5 \) | \( z = 500 \) | \( a = 1 \) |
| \( x = 10 \) | \( z = 1000 \) | \( a = 1 \) |
Influence of bias on activation
Bias \( b = 0 \)
| input | preactivation | activation |
|---|---|---|
| \( x = -10 \) | \( z = -10 \) | \( a = 0 \) |
| \( x = -5 \) | \( z = -5 \) | \( a = 0.01 \) |
| \( x = 0 \) | \( z = 0 \) | \( a = 0.5 \) |
| \( x = 5 \) | \( z = 5 \) | \( a = 0.99 \) |
| \( x = 10 \) | \( z = 10 \) | \( a = 1 \) |
Bias \( b = 5 \)
| input | preactivation | activation |
|---|---|---|
| \( x = -10 \) | \( z = -5 \) | \( a = 0.01 \) |
| \( x = -5 \) | \( z = 0 \) | \( a = 0.5 \) |
| \( x = 0 \) | \( z = 5 \) | \( a = 0.99 \) |
| \( x = 5 \) | \( z = 10 \) | \( a = 1 \) |
| \( x = 10 \) | \( z = 15 \) | \( a = 1 \) |
Bias \( b = -5 \)
| input | preactivation | activation |
|---|---|---|
| \( x = -10 \) | \( z = -15 \) | \( a = 0 \) |
| \( x = -5 \) | \( z = -10 \) | \( a = 0 \) |
| \( x = 0 \) | \( z = -5 \) | \( a = 0.01 \) |
| \( x = 5 \) | \( z = 0 \) | \( a = 0.5 \) |
| \( x = 10 \) | \( z = 5 \) | \( a = 0.99 \) |
- Rectangular strip with a pair of neurons
- Multiple strips
- Computing preactivation for desired sigmoid output
- Limitations of neural networks
Batching
- Problem with optimizing for a single sample
- Optimizing for a batch of samples
- Computational cost
- Updates count
Training with saturated sigmoid and mean square error cost function
| \( x = -2 \) | \( w = 3 \) | \( b = -1 \) |
Prediction
$$ z = wx + b $$
$$ z = (-2 * 3) - 1 $$
$$ z = -7 $$
$$ a = \sigma(-7) $$
$$ a = 0.000911 $$
Cost derivative w.r.t. activation
$$ y = 1 $$
$$ C = \frac{1}{2}(y - a)^2 $$
$$ \frac{ \partial{C} }{ \partial{a} } = a - y $$
$$ \frac{ \partial{C} }{ \partial{a} } = 0.000911 - 1 = -0.999089 $$
Cost derivative w.r.t. preactivation
$$ \frac{ \partial{C} }{ \partial{z} } =
\frac{ \partial{C} }{ \partial{a} } * \frac{ \partial{a} }{ \partial{z} } $$
$$ \frac{ \partial{C} }{ \partial{z} } = \frac{ \partial{C} }{ \partial{a} } * a * (1 - a) $$
$$ \frac{ \partial{C} }{ \partial{z} } = -0.999089 * 0.000911 * (1 - 0.000911) $$
$$ \frac{ \partial{C} }{ \partial{z} } = -0.00090934 $$
Cost derivative w.r.t. weight
$$ \frac{ \partial{C} }{ \partial{w} } = \frac{ \partial{C} }{ \partial{z} } *
\frac{ \partial{z} }{ \partial{w} } $$
$$ \frac{ \partial{C} }{ \partial{w} } = \frac{ \partial{C} }{ \partial{z} } * x $$
$$ \frac{ \partial{C} }{ \partial{w} } = -0.00090934 * -2 $$
$$ \frac{ \partial{C} }{ \partial{w} } = 0.00181868 $$
Cost derivative w.r.t. bias
$$ \frac{ \partial{C} }{ \partial{b} } = \frac{ \partial{C} }{ \partial{z} } * \frac{ \partial{z} }{ \partial{b} } $$
$$ \frac{ \partial{C} }{ \partial{b} } = -0.00090934 * 1 $$
$$ \frac{ \partial{C} }{ \partial{b} } = -0.00090934 $$
Weight update
$$ w = w - \alpha * \frac{ \partial{C} }{ \partial{w} } $$
$$ w = 3 - 1 * 0.00181868 $$
$$ w = 2.99818132 $$
Bias update
$$ b = b - \alpha * \frac{ \partial{C} }{ \partial{b} } $$
$$ b = -1 - (1 * -0.00090934) $$
$$ b = -0.99909066 $$
Prediction after updates
| \( x = -2 \) | \( w = 2.99818132 \) | \( b = -0.99909066 \) |
Binary cross-entropy cost function
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
Sample computations
\( y = 0 \) and \( a = 0 \)
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
$$ C = -( 0 + 1 * ln(1) ) $$
$$ C = -( 0 ) $$
$$ C = 0 $$
\( y = 0 \) and \( a = 1 \)
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
$$ C = -( 0 + 1 * ln(0) ) $$
$$ C = -( -\infty ) $$
$$ C = \infty $$
\( y = 1 \) and \( a = 0 \)
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
$$ C = -( 1 * ln(0) + 0 ) $$
$$ C = -( -\infty ) $$
$$ C = \infty $$
\( y = 1 \) and \( a = 1 \)
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
$$ C = -( 1 * ln(1) + 0 ) $$
$$ C = -( 0 ) $$
$$ C = 0 $$
Cost derivative w.r.t. activation
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
Call
$$ f = y*ln(a) $$
$$ g = (1 - y)*ln(1 - a) $$
Then
$$ C = -( f + g ) $$
$$ \frac{ \partial{C} }{ \partial{a} } =
-( \frac{ \partial{f} }{ \partial{a} } + \frac{ \partial{g} } { \partial{a} } ) $$
$$ f = y*ln(a) $$ $$ \frac{ \partial{f} }{ \partial{a} } = \frac{ y }{ a }$$
$$ g = (1 - y)*ln(1 - a) $$ $$ u = (1 - a) $$ $$ g = (1 - y)*ln(u) $$ $$ \frac{ \partial{g} } { \partial{a} } = \frac{ \partial{g} } { \partial{u} } * \frac{ \partial{u} } { \partial{a} } $$ $$ \frac{ \partial{g} } { \partial{a} } = \frac{ 1 - y } { u } * (-1) $$ $$ \frac{ \partial{g} } { \partial{a} } = - \frac{ 1 - y } { 1 - a } $$
$$ \frac{ \partial{C} }{ \partial{a} } = -( \frac{ \partial{f} }{ \partial{a} } + \frac{ \partial{g} } { \partial{a} } ) $$ $$ \frac{ \partial{C} }{ \partial{a} } = -( \frac{ y }{ a } - \frac{ 1 - y } { 1 - a } ) $$ $$ \frac{ \partial{C} }{ \partial{a} } = -( \frac{ y*(1 - a) - a*(1 - y) }{ a * (1 - a) } )$$ $$ \frac{ \partial{C} }{ \partial{a} } = -( \frac{ y - ay - a + ay }{ a * (1 - a) } )$$ $$ \frac{ \partial{C} }{ \partial{a} } = -( \frac{ y - a }{ a * (1 - a) } )$$ $$ \frac{ \partial{C} }{ \partial{a} } = \frac{ a - y }{ a * (1 - a) }$$
Cost derivative w.r.t. preactivation
$$ \frac{ \partial{C} }{ \partial{z} } =
\frac{ \partial{C} } { \partial{a} } * \frac{ \partial{a} } { \partial{z} } $$
$$ \frac{ \partial{C} }{ \partial{z} } = \frac{ a - y }{ a * (1 - a) } * a * (1 - a) $$
$$ \frac{ \partial{C} }{ \partial{z} } = a - y $$
Training with saturated sigmoid and binary cross-entropy cost function
| \( x = -2 \) | \( w = 3 \) | \( b = -1 \) |
Prediction
$$ z = wx + b $$
$$ z = (-2 * 3) - 1 $$
$$ z = -7 $$
$$ a = \sigma(-7) $$
$$ a = 0.000911 $$
Cost derivative w.r.t. preactivation
$$ y = 1 $$
$$ C = -( y*ln(a) + (1 - y)*ln(1 - a) ) $$
$$ \frac{ \partial{C} }{ \partial{z} } = a - y $$
$$ \frac{ \partial{C} }{ \partial{z} } = 0.000911 - 1 = -0.999089 $$
Cost derivative w.r.t. weight
$$ \frac{ \partial{C} }{ \partial{w} } = \frac{ \partial{C} }{ \partial{z} } *
\frac{ \partial{z} }{ \partial{w} } $$
$$ \frac{ \partial{C} }{ \partial{w} } = \frac{ \partial{C} }{ \partial{z} } * x $$
$$ \frac{ \partial{C} }{ \partial{w} } = -0.999089 * -2 $$
$$ \frac{ \partial{C} }{ \partial{w} } = 1.998178 $$
Cost derivative w.r.t. bias
$$ \frac{ \partial{C} }{ \partial{b} } = \frac{ \partial{C} }{ \partial{z} } * \frac{ \partial{z} }{ \partial{b} } $$
$$ \frac{ \partial{C} }{ \partial{b} } = -0.999089 * 1 $$
$$ \frac{ \partial{C} }{ \partial{b} } = -0.999089 $$
Weight update
$$ w = w - \alpha * \frac{ \partial{C} }{ \partial{w} } $$
$$ w = 3 - 1 * 1.998178 $$
$$ w = 1.001822 $$
Bias update
$$ b = b - \alpha * \frac{ \partial{C} }{ \partial{b} } $$
$$ b = -1 - (1 * -0.999089) $$
$$ b = -0.00091 $$
Prediction after updates
| \( x = -2 \) | \( w = 1.001822 \) | \( b = -0.00091 \) |
Softmax activation function
- Interpreting result of neural network with multiple output nodes
- Softmax function
$$ a_1 = \frac{ e^{z_1} } { e^{z_1} + e^{z_2} + e^{z_3} } $$ $$ a_2 = \frac{ e^{z_2} } { e^{z_1} + e^{z_2} + e^{z_3} } $$ $$ a_3 = \frac{ e^{z_3} } { e^{z_1} + e^{z_2} + e^{z_3} } $$
$$ e^{z_i} \ge 0 $$ $$ \sum_{j} e^{z_j} \ge 0 $$ $$ e^{z_i} \le \sum_{j} e^{z_j} $$ $$ a_i \in \lt 0, 1 \gt $$
$$ a_1 + a_2 + a_3 = \frac{ e^{z_1} } { e^{z_1} + e^{z_2} + e^{z_3} } + \frac{ e^{z_2} } { e^{z_1} + e^{z_2} + e^{z_3} } + \frac{ e^{z_3} } { e^{z_1} + e^{z_2} + e^{z_3} } $$ $$ a_1 + a_2 + a_3 = \frac{ e^{z_1} + e^{z_2} + e^{z_3} } { e^{z_1} + e^{z_2} + e^{z_3} } $$ $$ a_1 + a_2 + a_3 = 1 $$ $$ \sum_{j} a_j = 1 $$
Cross-entropy cost function
$$ C = - (\sum_j y_j * ln(a_j)) $$
$$ C = -y_i * ln(a_i) $$
$$ C = -ln(a_i) $$
Derivative of cross-entropy cost function w.r.t. preactivation of an active node
$$ \frac{ \partial{C} }{ \partial{a_i} } = - \frac{1}{a_i} $$
$$ \frac{ \partial{C} }{ \partial{a_1} } = - \frac{1}{a_1} $$
$$ a_1 = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } $$
$$ \frac{ \partial{f} }{ \partial{z_1} } = e^{z_1} $$ $$ \frac{ \partial{g} }{ \partial{z_1} } = e^{z_1} $$
$$ \frac{ \partial{a_1} }{ \partial{z_1} } = \frac{ (e^{z_1} * \sum_{j} e^{z_j}) - (e^{z_1} * e^{z_1})} { (\sum_{j} e^{z_j})^2 } $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = \frac{ e^{z_1} * ( \sum_{j} e^{z_j} - e^{z_1} ) } { (\sum_{j} e^{z_j})^2 } $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } * \frac{ \sum_{j} e^{z_j} - e^{z_1} } { \sum_{j} e^{z_j} } $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = a_1 * (1 - \frac{ e^{z_1} } { \sum_{j} e^{z_j} }) $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = a_1 * (1 - a_1) $$
$$ \frac{ \partial{C} }{ \partial{z_1} } = \frac{ \partial{C} }{ \partial{a_1} } * \frac{ \partial{a_1} }{ \partial{z_1} } $$ $$ \frac{ \partial{C} }{ \partial{a_1} } = - \frac{1}{a_1} $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = a_1 * (1 - a_1) $$ $$ \frac{ \partial{C} }{ \partial{z_1} } = - \frac{1}{a_1} * a_1 * (1 - a_1) $$ $$ \frac{ \partial{C} }{ \partial{z_1} } = - (1 - a_1) $$ $$ \frac{ \partial{C} }{ \partial{z_1} } = a_1 - 1 $$
$$ a_1 = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } $$
Call
$$ f = e^{z_1} $$
$$ g = \sum_{j} e^{z_j} $$
Then
$$ a_1 = \frac{ f } { g } $$
$$
\frac{ \partial{a_1} }{ \partial{z_1} } =
\frac{
\frac{ \partial{f} }{ \partial{z_1} } * g -
f * \frac{ \partial{g} }{ \partial{z_1} }
} {g^2}
$$
$$ \frac{ \partial{f} }{ \partial{z_1} } = e^{z_1} $$ $$ \frac{ \partial{g} }{ \partial{z_1} } = e^{z_1} $$
$$ \frac{ \partial{a_1} }{ \partial{z_1} } = \frac{ (e^{z_1} * \sum_{j} e^{z_j}) - (e^{z_1} * e^{z_1})} { (\sum_{j} e^{z_j})^2 } $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = \frac{ e^{z_1} * ( \sum_{j} e^{z_j} - e^{z_1} ) } { (\sum_{j} e^{z_j})^2 } $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } * \frac{ \sum_{j} e^{z_j} - e^{z_1} } { \sum_{j} e^{z_j} } $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = a_1 * (1 - \frac{ e^{z_1} } { \sum_{j} e^{z_j} }) $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = a_1 * (1 - a_1) $$
$$ \frac{ \partial{C} }{ \partial{z_1} } = \frac{ \partial{C} }{ \partial{a_1} } * \frac{ \partial{a_1} }{ \partial{z_1} } $$ $$ \frac{ \partial{C} }{ \partial{a_1} } = - \frac{1}{a_1} $$ $$ \frac{ \partial{a_1} }{ \partial{z_1} } = a_1 * (1 - a_1) $$ $$ \frac{ \partial{C} }{ \partial{z_1} } = - \frac{1}{a_1} * a_1 * (1 - a_1) $$ $$ \frac{ \partial{C} }{ \partial{z_1} } = - (1 - a_1) $$ $$ \frac{ \partial{C} }{ \partial{z_1} } = a_1 - 1 $$
Generic form
$$ \frac{ \partial{C} }{ \partial{z_i} } = a_i - 1 $$
Derivative of cross-entropy cost function w.r.t. preactivation of an inactive node
$$ \frac{ \partial{C} }{ \partial{z_2} } =
\frac{ \partial{C} }{ \partial{a_1} } * \frac{ \partial{a_1} }{ \partial{z_2} } +
\frac{ \partial{C} }{ \partial{a_2} } * \frac{ \partial{a_2} }{ \partial{z_2} } $$
$$ C = -ln(a_1) $$
$$ \frac{ \partial{C} }{ \partial{a_2} } = 0 $$
$$ \frac{ \partial{C} }{ \partial{z_2} } =
\frac{ \partial{C} }{ \partial{a_1} } * \frac{ \partial{a_1} }{ \partial{z_2} } $$
$$ a_1 = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } $$
$$ \frac{ \partial{f} }{ \partial{z_2} } = 0 $$ $$ \frac{ \partial{g} }{ \partial{z_2} } = e^{z_2} $$
$$ \frac{ \partial{a_1} }{ \partial{z_2} } = \frac{ 0 - (e^{z_1} * e^{z_2}) } { (\sum_{j} e^{z_j})^2 } $$ $$ \frac{ \partial{a_1} }{ \partial{z_2} } = - \frac{ e^{z_1} } { \sum_{j} e^{z_j} } * \frac{ e^{z_2} } { \sum_{j} e^{z_j} } $$ $$ a_1 = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } $$ $$ a_2 = \frac{ e^{z_2} } { \sum_{j} e^{z_j} } $$ $$ \frac{ \partial{a_1} }{ \partial{z_2} } = - a_1 * a_2 $$
$$ \frac{ \partial{C} }{ \partial{z_2} } = \frac{ \partial{C} }{ \partial{a_1} } * \frac{ \partial{a_1} }{ \partial{z_2} } $$ $$ \frac{ \partial{C} }{ \partial{a_1} } = - \frac{1}{a_1} $$ $$ \frac{ \partial{a_1} }{ \partial{z_2} } = - a_1 * a_2 $$ $$ \frac{ \partial{C} }{ \partial{z_2} } = - \frac{1}{a_1} * (- a_1 * a_2) $$ $$ \frac{ \partial{C} }{ \partial{z_2} } = a_2 $$
$$ a_1 = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } $$
Call
$$ f = e^{z_1} $$
$$ g = \sum_{j} e^{z_j} $$
Then
$$ a_1 = \frac{ f } { g } $$
$$
\frac{ \partial{a_1} }{ \partial{z_2} } =
\frac{
\frac{ \partial{f} }{ \partial{z_2} } * g -
f * \frac{ \partial{g} }{ \partial{z_2} }
} {g^2}
$$
$$ \frac{ \partial{f} }{ \partial{z_2} } = 0 $$ $$ \frac{ \partial{g} }{ \partial{z_2} } = e^{z_2} $$
$$ \frac{ \partial{a_1} }{ \partial{z_2} } = \frac{ 0 - (e^{z_1} * e^{z_2}) } { (\sum_{j} e^{z_j})^2 } $$ $$ \frac{ \partial{a_1} }{ \partial{z_2} } = - \frac{ e^{z_1} } { \sum_{j} e^{z_j} } * \frac{ e^{z_2} } { \sum_{j} e^{z_j} } $$ $$ a_1 = \frac{ e^{z_1} } { \sum_{j} e^{z_j} } $$ $$ a_2 = \frac{ e^{z_2} } { \sum_{j} e^{z_j} } $$ $$ \frac{ \partial{a_1} }{ \partial{z_2} } = - a_1 * a_2 $$
$$ \frac{ \partial{C} }{ \partial{z_2} } = \frac{ \partial{C} }{ \partial{a_1} } * \frac{ \partial{a_1} }{ \partial{z_2} } $$ $$ \frac{ \partial{C} }{ \partial{a_1} } = - \frac{1}{a_1} $$ $$ \frac{ \partial{a_1} }{ \partial{z_2} } = - a_1 * a_2 $$ $$ \frac{ \partial{C} }{ \partial{z_2} } = - \frac{1}{a_1} * (- a_1 * a_2) $$ $$ \frac{ \partial{C} }{ \partial{z_2} } = a_2 $$
Generic form
$$ \frac{ \partial{C} }{ \partial{z_k} } = a_k $$
Optimizing hidden layer activation function
- Sigmoid derivative and its effect on gradients across layers
- ReLU - rectified linear unit
- Derivative of ReLU
- Why not use a linear hidden activation?
Importance of weights initialization scheme
- Problem with naive weights initialization
- Scaling weights initialization w.r.t. input size
Tensorflow basics
- Why Tensorflow? Popularity, GPU processing, automatic differentiation
- Computational graph model
- Session
- Placeholders
- Variables
A good neural network implementation
Networks architectures
- Why deep networks?
- How broad should my layers be?
- Should I just use a big network for everything?
Training tips
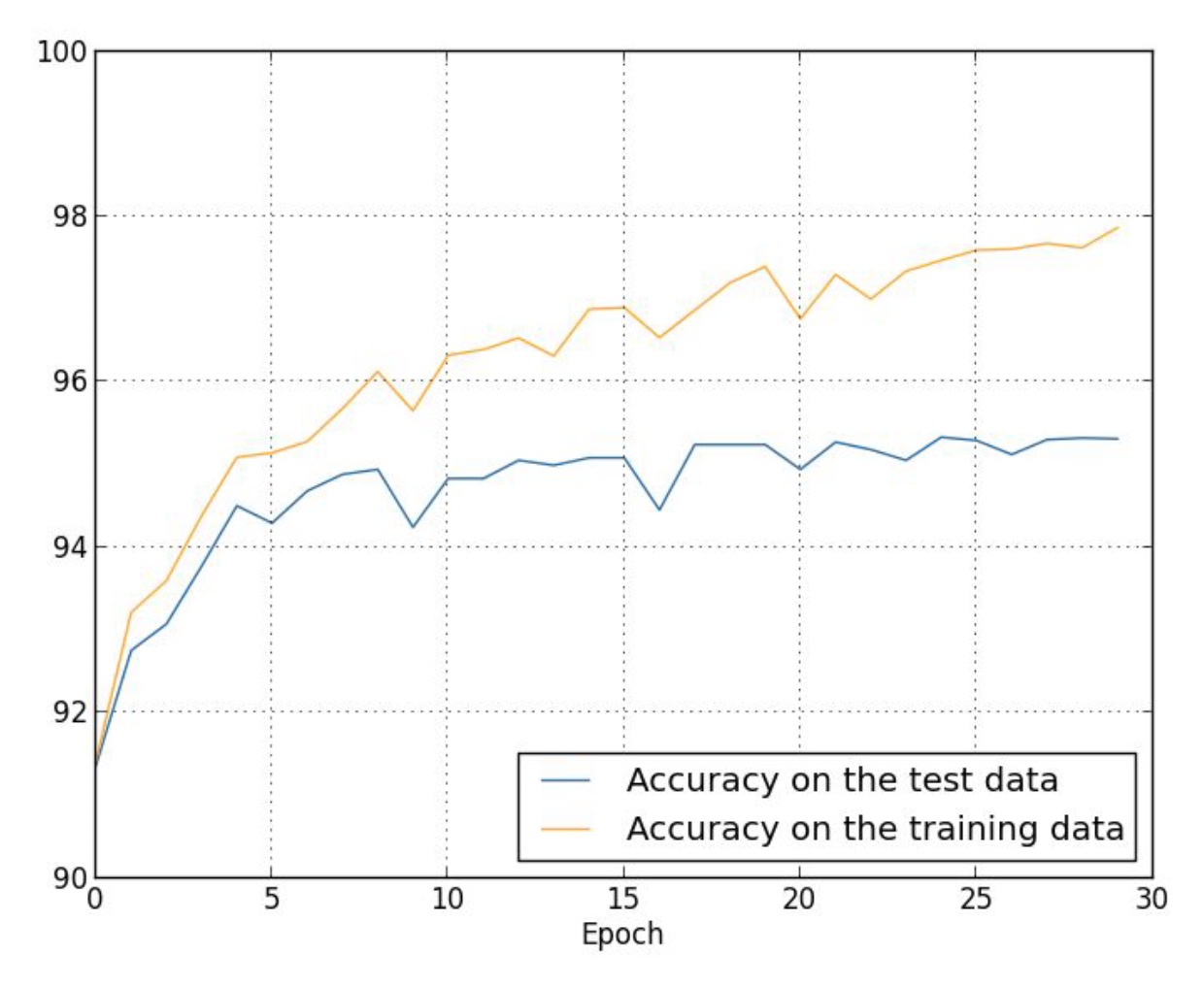
neuralnetworksanddeeplearning.com
- Check input and labels
- Check model
- Check loss definition
- Check learning rate
- Validation and overfitting
Beyond categorization networks
- Regression - real value prediction
- Mixing real values and categorical inputs
- Convolutional networks
- Recurrent networks
